Golden Ratio in Nature: 7 Stunning Examples

Examples of the golden ratio in nature span from the deep blue seas to the vast and expansive depths of outer space. Is this number part of a universal code?

There are many examples of the golden ratio in nature — yet many people have no idea what it is or how to appreciate the planet’s stunning geometry. This might be because the US as a nation, does not appear to excel in the subject of mathematics.

The New York Times reported that a 2012 study comparing numeracy levels among 16- to 65-year-olds in 20 countries found that Americans ranked in the bottom five. Some people argue this is because of how we are taught, while others find mathematics boring, complicated or difficult.

Looking at the golden ratio in nature brings mathematics to life  — quite literally — and it is far from boring. Don’t worry, we won’t over-complicate it, either! It becomes relatively easy to understand this mystical mathematical constant when we break it down.

Read on, and you might just find that mathematics is actually an elegant language that can help us understand the laws and magic of the universe — whether you are good with numbers or not!

The Golden Ratio in Nature, Art and Design

The golden ratio has a lot of interesting properties when we look at it in nature. It also has relevance in art, architecture and design. The Parthenon in Athens and Leonardo da Vinci’s Mona Lisa are regularly listed as examples of the golden ratio. Is it a coincidence that it shows up so often — particularly in places of beauty and intricacy? You can decide for yourself at the end of the article.

We see the golden ratio in nature, plants, animals, weather patterns and even in outer space. So, what exactly is the golden ratio?

Interested in the intersection between nature and human architecture? Check out our article on biophilic architecture and interior design or living in a geodesic dome house.

To Infinity and Beyond

In mathematics, the golden ratio is often represented as phi — which is a number. Phi isn’t just any old number, though — it’s an irrational number. In irrational numbers, the decimal goes on forever without repeating, meaning it essentially never ends. Irrational numbers are therefore, infinite numbers.

Another famous irrational number is pi — which we find by calculating the ratio of the circumference of any circle to its diameter. It doesn’t matter what size the circle is — the ratio of its circumference to its diameter will always be pi. The value of pi is usually written as 3.14 instead of its infinite 3.141592653589793238 … form. It’s important not to mix pi and phi up as they are completely different values.

Phi — the golden ratio — is numerically written as 1.618033988749895 … — or just 1.618 for short. It is also represented by the Greek letter φ. Other terms used to describe the golden ratio include:

• Golden Mean
• Extreme and Mean Ratio
• Golden Proportion
• Divine Proportion

Where Did the Golden Ratio Come From?

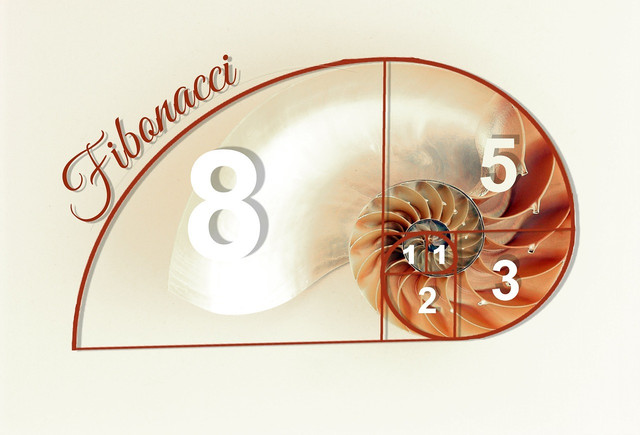
The golden ratio is derived from a famous — and very simple — mathematical sequence called the Fibonacci sequence. The sequence begins with the numbers 0 and 1 and we just add them together. Every number that follows in the pattern will be found by adding the two numbers before it.

So, we add:

0 + 1 = 1 1 + 1 = 2 1 + 2 = 3 2 + 3 = 5 3 + 5 = 8 5 + 8 =13 13 + 8 = 21

And so on.

Our sequence looks like this as it progresses into infinity: 0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…

Simple, right? That’s the first amazing thing about one of the most famous number sequences in the world — its simplicity. The second fascinating thing about Fibonacci numbers is, like the golden ratio in nature, that we see them everywhere.

On many plants, the number of petals is a Fibonacci number: For example, lilies have 3 petals, buttercups have 5 petals, delphiniums have 8, marigolds have 13, asters have 21 and daisies can be found with 34, 55 or even 89 petals.

We also see Fibonacci numbers in trees, leaves, branches, buds and many other places. According to fibonacci.com, even our bodies exhibit them: Your hands have 5 fingers on each hand, as there are five openings in the face. Many things, from bones in the body to evolution itself, show Fibonacci patterns.

DNA molecules measure 34 angstroms (a length unit) long by 21 angstroms wide for each full cycle of their double helix spiral. These numbers, 34 and 21, are both numbers in the Fibonacci series, and their ratio is 1.6190476 — which closely approximates the golden ratio.

When we look at even more accurate examples of the golden ratio in nature, these patterns become even more awesome.

Golden Spiral vs Fibonacci Spiral

The most amazing thing about the Fibonacci sequence is when we go beyond our only consecutive numbers in the sequence — 1,2 and 3 — and look at the rest of the numbers in ratio to each other (meaning we compare two numbers, usually by dividing them according to a formula) — we get 1.6.

Take any number in the sequence, then divide it by the number before it, and you will get 1.6. The further we progress through the sequence, the closer we get to exactly phi (1.618) — or the golden ratio.

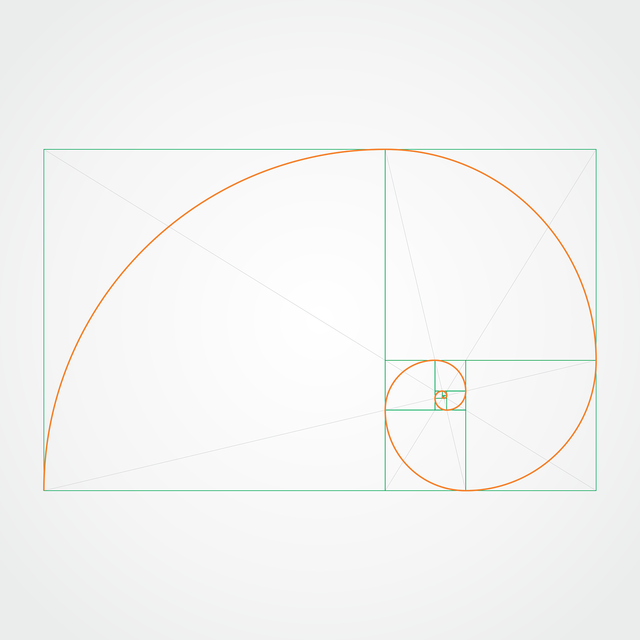
In geometry, golden ratios appears in many shapes — including rectangles, triangles and squares inside circles, and the pentagon. For example, if you take a square and multiple one side by 1.618 (the golden ratio), you will get a rectangle with perfectly harmonious proportions — called a golden rectangle.

When the golden ratio is applied as a growth factor constant to a spiral (meaning the spiral gets wider — or further from its origin — by a factor of the golden ratio (1.618) for every quarter turn it makes) we get the golden spiral.

The terms Fibonacci spiral and golden spiral are often used synonymously, but these two spirals are slightly different. A Fibonacci spiral is made by creating a spiral of squares that increase in size by the numbers of the Fibonacci sequence.

Because the Fibonacci numbers in ratio are so close to the golden ratio — 1.618 — the two spirals are almost identical. Some debate does exist among scholars about what exactly does constitute examples of the golden ratio in nature because of its likeness to the Fibonacci spiral. Both are considered logarithmic spirals.

1. Examples of the Golden Ratio in Nature: Space

 

The golden ratio in nature spirals through space and across our planet. Many argue that the logarithmic spiral phi generates when applied as a growth constant is visible in spiral galaxies throughout space. Our own galaxy — the Milky Way — is a spiral galaxy.

Going to the darkest regions of the universe, the golden ratio also seems to appear in black holes. In physics, phi is the exact point where a black hole’s modified heat changes from positive to negative.

The golden ratio is also associated with how planets, moons, asteroids and rings are distributed in the solar system.

2. Wind Spirals

Here on Earth, you might just see the golden ratio cooking up a storm. Hurricanes and cyclones all display the golden ratio at its most ferocious — whereby the perfect number can be seen spiraling around the eye of a perfect storm.

If you would like to know more about the eye of a cyclone or why they spin clockwise on one side of the globe and anti-clockwise on the other — check out our article on what is a hurricane exactly?

3. Leaves, Petals and Seeds: Pine Cones

In plant biology, the golden ratio and Fibonacci numbers have fascinated botanists for centuries. Phi controls the distribution and growth of leaves and other structures in many species — while others grow at a growth constant that is astonishingly close to this magic number.

For example, the ratio between two pine needles is 0.618, as well as the ratio of leaf venation. Pine cones are also an example of the golden ratio in nature. Again, we see a double set of spirals going in clockwise and anticlockwise directions. Both the spiral and number of them align with the golden ratio and Fibonacci numbers, respectively.

Leaves, petals and seeds that grow according to the golden ratio will not shade, overcrowd or overgrow each other — creating a very efficient growth pattern to flourish. This growth pattern will also promote maximum exposure to falling rain for leaves, or insects for pollination in the case of flowers. 

4. Sunflower Petals

Sunflowers are a stunning and perfect example of the golden ratio in nature. These beauties have 55 clockwise spirals and either 34 or 89 counterclockwise spirals — all Fibonacci numbers — growing at a constant of the golden ratio.

Researchers have also found evidence of the golden spiral and golden ratio is many other plants, including fiddleheads — the the curled up fronds of a young fern — daisies and spiral aloe vera.

5. Romanesco Broccoli

6. Golden Ratio in Animals: Horns, Tusks and Flying Patterns

The horns of certain animals — like some breeds of goat and sheep — grow according to phi. It is believed to be found in the curvature of elephant tusks and the shape of a kudu’s horn among others.

Chameleon and seahorse tails display similar formations upside-down, which is also close to the golden ratio.

Many falcons, eagles and other raptors follow a golden spiral when attacking their prey — which optimizes their ability to fly and see their prey at the same time as their eyes are at the sides of their heads. 

Many seashells and shell-life also exhibit beautiful, spiral patterns. The nautilus shell is one of the most famous and commonly cited examples of the golden ration in nature. If you’d like to have an example of this stunning geometry of nature in your home, check out our guide: Shell Collecting the Legal, Ethical, Eco-Friendly Way.

The inner part of the ear of mammals — called the cochlea — carries sound through a golden tunnel.

7. Bee Ancestry

Finally, our favorite example of the golden ratio in nature is among some of our hardest workers on the planet — bees. Their ancestral tree always follows the Fibonacci sequence of numbers! Many researchers and authors believe that the elliptical honeycomb of a hive is also related to the golden ratio. If bees become extinct, humans and many other examples of the golden ratio in nature will be at serious risk of extinction, too.

Read more:

• Tropical Rainforest Ecosystems: Why Are They Important?
• 8 Things You Can Do to Save the Ocean
• Native Gardening for Wildlife: Benefits and Tips for Beginners

** Links to retailers marked with ** or underlined orange are partially partner links: If you buy here, you actively support Utopia.org, because we will receive a small part of the sales proceeds. More info.

Tags: Animals Guide Natural Outdoors